Contoh Soal Termodinamika (Bagian II)
Soal 1
Hitung
perubahan entropi ketika 3,00 mol bensin menguap secara reversibel pada titik
didih normalnya yaitu 80,1°C. Entalpi molar penguapan bensin pada suhu ini
adalah 30,8 kJ mol-1. (Ketika penguapan terjadi, tekanan bensin di
atas cairan dipertahankan pada 1 atm dengan cara meningkatkan volume yang
tersedia untuk gas.)
Solusi:
Perubahan
entropi dari suatu proses reversibel diberikan oleh rumus:
ΔS = qrev/T
di mana ΔS
adalah perubahan entropi, qrev adalah kalor yang diserap atau dilepaskan
selama proses reversibel, dan T adalah suhu pada saat proses terjadi.
Pada kasus
ini, bensin menguap secara reversibel pada titik didih normalnya yaitu 80,1°C.
Karena tekanannya dipertahankan pada 1 atm dengan meningkatkan volume yang
tersedia untuk gas, proses ini bersifat isobarik. Kalor yang diserap oleh
bensin selama penguapan diberikan oleh entalpi molar penguapan, ΔH_vap:
qrev
= ΔHvap × n
di mana n
adalah jumlah mol bensin yang menguap. Pada kasus ini, n = 3,00 mol.
qrev
= (30,8 kJ/mol) × (3,00 mol) = 92,4 kJ
Suhu pada
saat proses terjadi adalah titik didih bensin, yang diberikan sebagai 80,1°C.
Suhu ini harus dikonversi ke kelvin:
T = 80,1°C
+ 273,15 = 353,25 K
Sekarang
kita dapat menghitung perubahan entropi:
ΔS = qrev/T
= (92,4 kJ)/(353,25 K) = 0,262 kJ/K
Oleh karena
itu, perubahan entropi ketika 3,00 mol bensin menguap secara reversibel pada titik
didih normalnya yaitu 80,1°C adalah 0,262 kJ/K.
Soal 2
(a) Hitung
perubahan entropi untuk proses 5,00 mol argon yang mengembang secara reversibel
pada suhu konstan 298 K dari tekanan 10,0 atm menjadi 1,00 atm.
(b) Hitung
perubahan entropi untuk keadaan awal dan akhir yang sama seperti pada bagian
(a) tetapi melalui jalur yang berbeda. Pertama, 5,00 mol argon mengembang
secara reversibel dan adiabatik antara dua tekanan yang sama. Ini menyebabkan
suhu turun menjadi 118,6 K. Kemudian gas dipanaskan pada tekanan konstan
kembali ke 298 K.
Solusi:
(a) Untuk
menghitung perubahan entropi untuk proses tersebut, kita dapat menggunakan
rumus:
ΔS = nR ln(V2/V1)
= nR ln(P1/P2)
Di mana ΔS
adalah perubahan entropi, n adalah jumlah mol, R adalah konstanta gas, V1
adalah volume awal, V2 adalah volume akhir, P1 adalah tekanan awal, dan P2
adalah tekanan akhir.
Oleh karena
itu, perubahan entropi adalah:
ΔS = nR ln(P1/P2)
= (5,00 mol)(8,314 J/mol·K)ln(10 atm/1 atm) = +95,7 J/K
(b) Untuk
langkah pertama, prosesnya adiabatik, sehingga tidak ada pertukaran kalor dan
ΔS = 0. Ketika gas dipanaskan secara reversibel pada tekanan konstan dari 118,6
hingga 298 K, perubahan entropinya adalah
ΔS = nCp ln(T2/T1)
Di mana C
adalah kapasitas kalor molar gas pada tekanan konstan. Untuk gas ideal, kita dapat
hitung menggunakan rumus:
Cp = (5/2)R
Jadi:
ΔS1 = (5,00
mol)(5/2)(8,314 J/mol·K)ln(298K/118,6 K) = +95,7 J/K
Soal 3:
Hitunglah
panas yang diserap dan kerja yang dilakukan pada sistem gas ideal yang terdiri
dari 5,00 mol saat mengalami ekspansi yang ireversibel pada suhu konstan T
sebesar 298 K dari tekanan 10,0 atm hingga 1,00 atm. Tekanan eksternal dijaga
konstan pada 1,00 atm.
Solusi:
Pertama
kita hitung volume awal menggunakan persamaan gas ideal:
V1
= nRT/P1 = (5 mol) (0,08206 L.atm.K-1.mol-1)(298K)/10
atm = 12,2 L
Lalu kita
hitung volume akhir:
V2
= nRT/P1 = (5 mol) (0,08206 L.atm.K-1.mol-1)(298K)/1
atm = 122 L
Selanjutnya
hitung kerja yang dilakukan menggunakan rumus:
wirrev
= -Pext ΔV = - (1,00 atm) (122 L – 12,2 L) =
109,8 L.atm = -11,125 kJ
Pada T
konstan, ΔU
= 0, sehingga
qirrev
= - wirrev = 11,125 kJ
Soal 4
Diketahui:
So(N2(g))
= 191,50 JK-1mol-1
So(O2(g))
= 205,03 JK-1mol-1
So(NO2(g))
= 239,95 JK-1mol-1
Hitung ΔSo untuk reaksi kimia
Dengan reaktan
dan produk berada pada suhu 25oC dan tekanan 1 atm.
Solusi:
Perubahan entropi untuk reaksi adalah jumlah entropi produk, dikurangi jumlah entropi reaktan, masing-masing dikalikan dengan koefisien dalam persamaan kimia seimbang.
Soal 5
Diketahui:
ΔGfo(N2O(g))
= 104,18 kJ.mol-1
ΔGfo(NO2(g))
= 51,29 kJ.mol-1
ΔGfo(NO(g))
= 86,55 kJ.mol-1
Hitung ΔGo untuk reaksi kimia



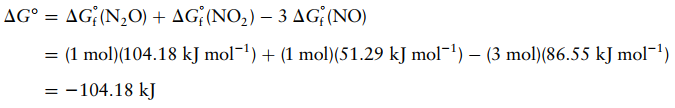


Tidak ada komentar:
Posting Komentar